[ad_1]
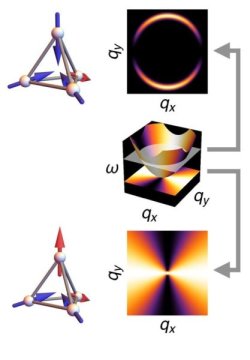
When physicists send neutrons shooting through a frustrated magnet, the particles spray out the other side in signature patterns. The designs appear because, even at low temperatures, atoms in a frustrated metal oscillate in time with each other. One distinctive pattern, known as a “pinch point,” resembles a bow-tie and holds wide acclaim in the world of spin liquids. Pinch points are often accompanied by unsung crescent patterns called “half moons,” but the physics linking the phenomena has never been clarified.
Now, researchers at the Okinawa Institute of Science and Technology Graduate University (OIST) have revealed that pinch points and half moons are one and the same — simply signatures of the same physics at different energy levels. Their unified theory, published October 12, 2018, as a Physical Review B Rapid Communication, is the first to explain the underlying physics driving the often paired phenomena.
“The theory itself is kind of simple,” said Han Yan, a graduate student in the Theory of Quantum Matter Unit at OIST and first author of the study. “From the same theory that gives you the pinch point at lower energy, you can calculate what happens at higher energy — and you get a pair of half moons.”
If you zoom in close to a frustrated magnet, each atom making up the material seems to spin erratically. In reality, however, these atoms take part in a beautifully coordinated dance, turning in time with each other so that their magnetic pulls ultimately cancel out. This ballet is difficult to observe directly, so instead, physicists search for telltale clues that the performance is taking place.
An experimental technique called neutron scattering allows scientists to gather these clues. Neutrons carry no electric charge, but they do act as a localized source of magnetism. Individual atoms also act as tiny magnets, complete with their own north and south poles. When sent whizzing through a material, a neutron’s speed and direction is thrown off by the atoms it passes, and thus it is “scattered.”
The pattern of the scattering tells physicists how atoms are behaving inside a material. For instance, if neutrons scatter helter-skelter, physicists infer that the atoms within a material are aligned randomly. If neutrons scatter in a hallmark bow-tie, they infer that the atoms are twirling in tandem, as they would in a frustrated magnet.
Pinch points appear when an equal number of atomic magnets, or “spins,” are pointing “out” as pointing “in” in any region of the frustrated magnet. This equilibrium renders the material non-magnetic and maintains it at a minimal level of energy.
Half moons appear when a frustrated magnet has energy beyond this minimal level, and thus violates the local conservation law which requires an equal number of spins be pointed out as in. In essence, half moons are pinch points set on a curve. The greater the curvature, the stronger the violation, the more energy the system is using. The OIST researchers uncovered this relationship in their calculations and later put it to the test.
The researchers tested their unified theory in a simulated system where pinch points and half moons can be observed together, known as a Heisenberg antiferro-magnet on a kagome lattice. They also applied their equations to recent observations of the frustrated magnet Nd2Zr2O7 and found that their theory explained the appearance of the two patterns in application, as well.
“Pinch points and half moons come from the same underlying physics — one from respecting the local conservation law and the other from violating it,” said Yan. “When you put them together, they form a whole picture of the overall phenomenology.”
In the future, the unified theory of half moons and pinch points should prove useful in both theoretical and applied physics, and perhaps beyond.
“From a certain point of view, each condensed matter system is unto itself a different universe,” said Yan. “It’s a great intellectual curiosity to find these universes, with their own strange laws of nature, but it also relates to daily life. People are trying to identify the particularly useful laws in these mini-universes so we might use them to our advantage.”
[ad_2]