[ad_1]
How did the zebra get its stripes, or the leopard its spots? Humankind has been trying to answer such questions since our earliest recorded days, and they resonate throughout the extant mythologies and folklores of an earlier world. In modern times, we’ve looked to mathematical models and most recently to genomic science to uncover the explanation of how patterns form in living tissues, but a full answer has proven particularly hard to get at.
The mechanism of pattern formation in living systems is of paramount interest to bioengineers seeking to develop living tissue in the laboratory. Engineered tissues would have countless potential medical applications, but in order to synthesize living tissues, scientists need to understand the genesis of pattern formation in living systems.
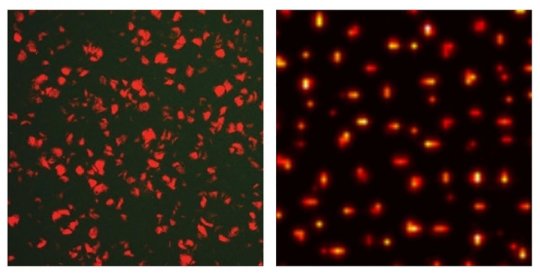
A new study by researchers at the University of Illinois at Urbana-Champaign, the Massachusetts Institute of Technology, and the Applied Physics Laboratory, Johns Hopkins University has brought science one step closer to a molecular-level understanding of how patterns form in living tissue. The researchers engineered bacteria that, when incubated and grown, exhibited stochastic Turing patterns: a “lawn” of synthesized bacteria in a petri dish fluoresced an irregular pattern of red polka dots on a field of green.
What are classic Turing patterns?
Turing patterns can be stripes, spots or spirals that arise naturally out of a uniform state. In 1952, the British mathematician, computer scientist, and theoretical biologist Alan Turing proposed a mechanism for how patterns form, theorizing that it’s due to a very general kind of instability, which he worked out mathematically. At that time, biology had not yet uncovered the complexities of gene regulation, and it’s now clear that the model Turing proposed is overly simplified to describe the multitude of parameters at work in animal-skin pattern formation. So while Turing patterns have been observed in certain chemical reactions, such patterns have proven very difficult to demonstrate in biological organisms.
U of I Physics Professor Nigel Goldenfeld illustrates the limitations of classic Turing pattern formation in biology, using a predator-prey analogy.
“The problem with Turing’s mechanism,” Goldenfeld explains, “is that it hinges on a criterion that isn’t satisfied in many biological systems, namely that the inhibitor must be able to move much more quickly than the activator. For example, if instead of chemicals, we were looking at two creatures in an ecosystem, like wolves and sheep, the wolves would need be able to move around much faster than the sheep to get classic Turing patterns. What this would look like, you would first see the sheep grow in number, feeding the wolves, which would then also grow in number. And the wolves would run around and contain the sheep, so that you would get little localized patches of sheep with the wolves on the outside. That’s essentially the mechanism in animal terms for what Turing discovered.”
The stochastic Turing model is driven by randomness.
In the current study, the researchers demonstrated both experimentally and theoretically that Turing patterns do in fact occur in living tissues — but with a twist. Where the instability that generates the patterns in Turing’s model is defined as a high diffusion ratio between two chemicals, an activator and an inhibitor, in this study, researchers demonstrate that it’s actually randomness — which would in most experiments be considered background noise — that generates what Goldenfeld has coined a stochastic Turing pattern.
About a decade ago, Goldenfeld and a former graduate student, Dr. Tom Butler, developed a theory of stochastic Turing patterns, wherein patterns develop not from a high inhibitor-activator ratio, but from the noise of stochastic gene expression. Goldenfeld explains, “About 10 years ago we asked, what happens if there is only a small number of sheep, so that there are large fluctuations in population numbers? Now you get processes where sheep die at random. And we discovered, when you give birth to randomness, that actually drives the formation of stochastic Turing patterns. These are random patterns, but they have a very characteristic structure, and we worked out mathematically what that was.
“The theory of stochastic Turing patterns doesn’t require a great difference in speed between the prey and the predator, the activator and the inhibitor. They can be more or less the same, and you still get a pattern. But it won’t be a regular pattern. It’ll be disordered in some way.”
The bioengineering experiments
The bacterial patterning experiments in this study were being performed around the same time Goldenfeld and Butler were developing their theory. The initial motivation for the in vivo study was to see whether bacteria could be engineered to produce a Turing instability. The researchers used synthetic biology to engineer bacteria, based on the activation-inhibition idea from Turing. They injected the bacteria with genes that made the bacteria emit and receive two different molecules as signals. The researchers attached fluorescent reporters to the molecules, creating a system where they could view the on/off switch of the genetic circuits through their signaling molecules: the activator fluoresced red and the inhibitor green. The researchers observed that, starting with a homogeneous film, the engineered bacteria formed red dots surrounded by a field of green after incubation for a period of time — but the bacteria formed irregular Turing patterns, like those predicted by the stochastic theory.
The original experimental and modeling work at MIT were led by Ron Weiss and carried out by David Karig, now at the Applied Physics Laboratory, Johns Hopkins University, and Ting Lu, now at the U of I, and later continued by graduate student Nicholas DeLateur at MIT.
Goldenfeld notes, “Serendipity definitely played a role in our connecting our two studies, as it often does in academia — the right place, the right time, and our ideas converged.”
Validating the stochastic Turing theory
To test if the experiments really were described by the new theory took several years of work. K. Michael Martini, a graduate student at the Center for the Physics of Living Cells at the U of I, worked with Goldenfeld to build a very detailed stochastic model of what was going on in these synthetic pattern-forming gene circuits, computed the consequences, and then compared the theoretical predictions with what the bioengineers had seen in the petri dishes.
“To really prove that our stochastic patterns work — it was hard. We had a lot of predictions we had made that had to be verified in experiment,” comments Goldenfeld. “Because the mathematics that describe these patterns have many parameters, we had to explore all of the effects of each. It involved a lot of searching in parameter space to reveal what was the mechanism of pattern formation. And there was necessarily a lot of interaction and collaboration with our engineering colleagues.
“What our work shows is that you can in fact get Turing patterns even in situations where you wouldn’t expect to be able to see them, but they are disordered patterns — stochastic Turing patterns. And the stochasticity here is not the birth and death of sheep or wolves, but it’s the birth and death, the creation and absorption of proteins. This is a very counter-intuitive prediction: It’s the noise of stochastic gene expression that generated these patterns. Normally you think of noise wiping out a signal. If you were trying to listen to music on radio, noise in the signal drowns it out. But in this case, we have a noise-stabilized pattern.”
These findings shed new light on an age-old question and begins to pave the way for future efforts in biomedical engineering.
Goldenfeld affirms, “This is really the first proof of principle that you can engineer in vivo stochastic Turing patterns, though it’s not simple. So now we know that this mechanism really can work, and that these fluctuations can drive patterns. Ultimately, bioengineers would like to use this type of technology to make novel tissues and new functional biological systems. Our study shows that you can do that in a regime where the classical Turing patterns couldn’t be used.”
[ad_2]